箱形图
1. 简介
箱形图又称盒须图、盒式图或箱线图,是一种用作显示一组数据分布情况的统计图。
如果一个数据集中包含了一个分类变量和一个或者多个连续变量,那么你可能会想知道连续变量会如何随着分类变量水平的变化而变化,而箱形图就可以提供这种方法,它只用了 5 个数字对分布进行概括,即一组数据的最大值、最小值、中位数、下四分位数及上四分位数。对于数据集中的异常值,通常会以单独的点的形式绘制。箱形图可以水平或者垂直绘制。
箱形图多用于数值统计,虽然相比于直方图和密度曲线较原始简单,但是它不需要占据过多的画布空间,空间利用率高,非常适用于比较多组数据的分布情况。
从箱形图中我们可以观察到:
- 一组数据的关键值:中位数、最大值、最小值等。
- 数据集中是否存在异常值,以及异常值的具体数值。
- 数据是否是对称的。
- 这组数据的分布是否密集、集中。
- 数据是否扭曲,即是否有偏向性。
注:当图上存在多个箱形图,可以使用颜色区分来对多个数据集数据的分布情况做对比。
英文名:Box Chart
2. 箱形图的应用场景
例子 1:关注于一组数据的分布情况
这里我们以经典的鸢尾花数据为例。
| 品种 | 萼片长度 | 萼片宽度 | 花瓣长度 | 花瓣宽度 |
|---|---|---|---|---|
| I. setosa | 4.3 | 3.0 | 1.1 | 0.1 |
| I. versicolor | 5.7 | 2.8 | 4.1 | 1.3 |
| I. virginica | 6.7 | 3.3 | 5.7 | 2.1 |
| ... | ... | ... | ... | ... |
如下图,我们用箱形图将不同种类的鸢尾花的花萼和花瓣的长度、宽度数据展示出来,同时我们还可以比较不同品种间花瓣和萼片数据是如何变化的。
例子 2:分组箱形图
为了更清晰得比较不同品种间相同属性数值的区别,可以将上图变化为如下二维多个箱形图形式。
例子 3: 一维箱形图
箱形图有多种变换,这里介绍下一维箱形图,下图还以鸢尾花数据为例,展示的是所有品种的花萼和花瓣长度、宽度的情况,虽然是在一维坐标系中,但是通过添加颜色属性,可以为该一维箱形图再增加一个展示维度,即分类。
附录: 箱形图的构成
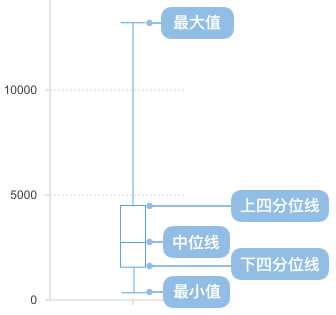
| 图表类型 | 箱形图 |
|---|---|
| 适合的数据 | 一个分类字段,一个连续字段 |
| 功能 | 观察数据的分布情况 |
| 数据与图形的映射 | 分类字段映射到横轴 对连续字段经过分位统计后,得出最大值、最小值、上四分位、下四分位、中位线这四个元数据。然后将它们分别进行如右图映射到纵轴。 |
| 适合的数据条数 | 小于12*N (N是分组数,大于12条会影响到文本排布,不利于阅读) |